Погрешности при измерении физических величин
При измерении любой физической величины принципиально невозможно определить ее истинное значение. Погрешности измерений могут быть связаны с техническими трудностями (несовершенство измерительных приборов, ограниченные возможности зрительного аппарата человека, с помощью которого во многих случаях регистрируются показания приборов, и т.д.), а также с целым рядом факторов, которые трудно или невозможно учесть (колебания температуры воздуха, движение потоков воздуха вблизи измерительного прибора, вибрации измерительного прибора вместе с лабораторным столом и т.п.).
Разность между измеренным и истинным значениями физической величины называется погрешностью (ошибкой) измерения.
Методические погрешности обусловлены недостатками применяемого метода измерения, несовершенством теории физического явления, к которому относится измеряемая величина, неточностью расчетной формулы. Например, при взвешивании тела на аналитических весах методическая ошибка может быть связана с тем, что не учитывается разность выталкивающих сил, действующих со стороны окружающего воздуха на тело и разновесы. Методические погрешности могут быть уменьшены при изменении и усовершенствовании метода измерения, а также введением уточнений или поправок в расчетную формулу.
Приборные погрешности обусловлены несовершенством конструкции и неточностью изготовления измерительных приборов. Например, ход секундомера может изменяться при резких колебаниях температуры, центр шкалы секундомера может не точно совпадать с осью вращения его стрелки и т.д. Уменьшение приборной погрешности достигается применением более точных (но вместе с тем и более дорогостоящих) приборов. Полностью устранить приборную погрешность невозможно.
Случайные погрешности вызываются многими факторами, не поддающимися учету. Например, на показания чувствительных рычажных весов могут повлиять:
- вибрации здания от проезжающих по улице автомобилей
- пылинки, оседающие на чашки весов во время взвешивания
- удлинение одной половины коромысла весов, вблизи которой находится рука экспериментатора
- и т.д.
Полностью избавиться от случайных погрешностей невозможно, но их можно уменьшить за счет многократного повторения измерений. При этом влияние факторов, приводящих к завышению и занижению результатов измерений, может частично компенсироваться. Расчет случайных погрешностей производится на основе теории вероятностей.
В качестве результата измерения какой-либо физической величины принимают среднее арифметическое Аср серии из n измерений:
Модуль отклонения результата i-го измерения Аi от среднего арифметического Аср называется абсолютной погрешностью данного измерения:
Средней абсолютной погрешностью величины Аср серии из n измерений называется величина:

Для сравнения точности измерения физических величин подсчитывают относительную погрешность Е (которую обычно выражают в процентах):
Окончательно результат измерения физической величины А представляют в виде:
причем в качестве абсолютной погрешности АА принимают наибольшую из средней абсолютной и приборной погрешностей (в более строгих расчетах погрешность АА выбирают на основании сопоставления случайной и приборной погрешностей). Подобная запись говорит о том, что истинное значение измеряемой величины заключено в интервале от Аср — ▵А до Аср + ▵А.
На шкалах многих измерительных приборов указывается так называемый класс точности. Условным обозначением класса точности является цифра, обведенная кружком. Класс точности определяет абсолютную приборную погрешность в процентах от наибольшего значения величины, которое может быть измерено данным прибором. Например, амперметр имеет шкалу от 0 до 5 А, его класс точности равен 1,0. Абсолютная погрешность измерения силы тока таким амперметром составляет 1,0 % от 5 А, т.е. ▵Априб =±0,05 А.
Если класс точности на шкале прибора не указан, то абсолютную погрешность прибора обычно принимают равной половине цены наименьшего деления шкалы прибора. Например, абсолютная погрешность измерения длины миллиметровой линейкой часто принимается равной ±0,5 мм.
При определении абсолютной погрешности прибора по цене деления следует обращать внимание на то, как производится измерение данным прибором, чем и как регистрируются результаты измерения, каково расстояние между соседними штрихами на шкале прибора и т.д. Если, например, расстояние от пола до подвешенного на нити груза измеряется с помощью миллиметровой линейки без каких-либо указателей, визиров и т.п., то абсолютная погрешность измерения не может быть принята меньшей 1 мм. Приборная погрешность принимается равной цене деления и в тех случаях, когда деления на шкале прибора нанесены очень часто, когда указателем прибора является не плавно перемещающаяся, а «скачущая» стрелка (как, например, у ручного секундомера), и т.д.
Рассмотрим пример обработки результатов прямых измерений. При прямом измерении некоторой физической величины А выполняют следующие действия:
- измеряют физическую величину n раз (А1, А2, …, Аn)
- находят среднее значение измеряемой величины Аср по формуле
- находят абсолютные погрешности каждого измерения и среднюю абсолютную погрешность всей серии измерений по формуле; в качестве абсолютной погрешности берут либо среднюю абсолютную погрешность, либо приборную погрешность (в зависимости от того, какая из этих погрешностей больше)
- записывают результаты измерений в виде, представленном формулой
- округляют абсолютную погрешность результата до двух значащих цифр, если первая из них 1 или 2, и до одной значащей цифры во всех остальных случаях; среднее значение измеряемой величины округляется или уточняется
- подсчитывают относительную погрешность результата
Пример. Измерение диаметра d шарика производилось пять раз с помощью микрометра, абсолютная погрешность которого dприб = ±0,01 мм. Результаты измерения диаметра шарика: d1= 5,27 мм, d2 = 5,30 мм, d3 = 5,28 мм, d4 = 5,32 мм, d5 = 5,28 мм.
Находим среднее значение диаметра шарика:
dср = (5,27 + 5,30 + 5,28 + 5,32 + 5,28)/5 = 5,29 мм.
Абсолютные погрешности измерений равны: ▵d1 = 0,02 мм, ▵d2 = 0,01 мм, ▵d3 = 0,01 мм, ▵d4 = 0,03 мм, ▵d5 = 0,01 мм, а средняя абсолютная погрешность:
▵dср = (0,02 + 0,01 + 0,01 + 0,03 + 0,01)/5 = 0,016 мм.Поскольку средняя абсолютная погрешность больше приборной, результат измерения d = (5,290 ± 0,016) мм.
Относительная погрешность измерения диаметра шарика
Е = 0,016 / 5,29 =0,003 = 3 %.

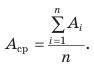


Добавить комментарий